步骤：

（1）建系：建立适当的坐标系，用有序实数对（x,y）表示曲线上任意一点M的坐标；

（2）设点：写出适合条件的p（M）的集合P={M|p(M)}；

（3）表示:用坐标表示条件p(M)，列出方程F(x,y)=0；

（4）化简：化方程f(x,y)=0为最简形式；

（5）下结论：说明以化简后的方程的解为坐标的点都在曲线上。

化简前后方程的解集是相同的，步骤（5）可以省略不写，如有特殊情况，可以适当说明。

另外，也可以根据情况省略（2），直接列出曲线方程。

（1）如果能够确定动点的轨迹满足某一直曲线的定义，则可根据曲线的定义直接写出方程。

（2）如果动点的轨迹与圆锥曲线有关，则可运用圆锥曲线定义求出动点的轨迹方程。

如果所求轨迹中的动点，随着另一动点的运动而运动，而另一动点有在某条已知曲线上，常设法利用轨迹中的动点坐标（x,y)，表示已知曲线上动点的坐标（x1,y1)，再将它代入已知曲线的方程即可。

如果很难找出动点坐标满足的关系，可借助中间变量——参数，建立起动点坐标x，y之间的联系，然后消去参数得到曲线方程。

步骤一般为：

引入参数——建立参数方程——消去参数，得到等价的普通方程。

如果所求轨迹上的动点，是两条动曲线的交点，可用两曲线的方程联立解得。

例题 ：

2.在同一坐标系中画出下列抛物线，观察它们开口的大小，并说明抛物线开口大小与方程中x的系数的关系：

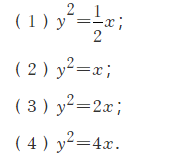
解析：

1.

2.