(1)定义:已知两个非零向量a,b,则|a||b|cos〈a,b〉叫做a,b的数量积,记作a·b.
(2)数量积的运算律
数乘向量与向量数量积的结合律 | (λa)·b=λ(a·b) |
交换律 | a·b=b·a |
分配律 | a·(b+c)=a·b+a·c |
(3)空间向量的夹角
①定义:已知两个非零向量a,b,在空间任取一点O,作→=a,→=b,则∠AOB叫做向量a与b的夹角,记作〈a,b〉.②范围:〈a,b〉∈[0,π].特别地:当〈a,b〉=2时,a⊥b.
(4)空间向量的数量积的性质

设两个向量坐标表示分别是(x1,y1,z1)、(x2,y2,z2)(均不是零向量).
①垂直就是点乘为0,只要记住点乘的定义:每个坐标分量对应着乘再相加.所以垂直的公式就是x1x2+y1y2+z1z2=0
②平行的坐标表示,就是对应坐标分量成比例,x1:x2=y1:y2=z1:z2
(1)两点间距离公式:已知两点坐标A(x₁,y₁)与 B(x₂,y₂),则线段AB之间的距离为:
AB=d=√[(x₂ - x₁)²+(y₂ - y₁)²] (即两点横、纵坐标的差的平方和的算术平方根)
(2)中点公式:已知A(x₁,y₁)与 B(x₂,y₂),则线段AB的中点M的坐标为:
M ( (x₁ + x₂)/2,(y₁ + y₂)/2 ) (中点公式是求一条线段的中点坐标公式)
例题 :
1.由代数式的乘法法则类比推导向量的数量积的运算法则:


2.由代数式的乘法法则类比推导向量的数量积的运算法则,正确的选项有 :
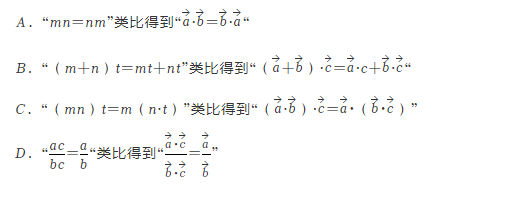
3.

4.以下命题正确的个数为 .

5.

6.

解析:
1.

2.

3.

4.

5.

6.

2022年致尚职教高考共500名学子参加了3+证书高考,300分以上人数共计177人,300分优秀率达35.4%,2022年广东省3+证书高考人数12.3万人300分以上人数约11200人,优秀率仅9%,致尚职教高考优秀率是全省优秀率的3.93倍。
致尚升本www.zssbjy.com 聚焦于成人学历提升培训(高职高考、专插本、高考复读等),秉承“做好课程做好老师、做好服务”的价值主张,通过科学的管理、雄厚的师资力量、别具一格的教学特色,先后帮助了一批又一批学子圆梦大学。
