1)了解向量的概念、向量的长度（模）和单位向量理解相等向量、负向量、平行（ 共线）向量的意义。
2)理解向量的加法与减法运算及其运算法则。
1.向量的概念：
既有大小又有方向的量，注意向量和数量的区别。向量常用有向线段来表示，注意不能说向量就是有向线段，为什么？（向量可以平移）。
2．零向量：
长度为0的向量叫零向量，记作：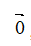
，注意零向量的方向是任意的；
3．单位向量：
长度为一个单位长度的向量叫做单位向量(与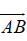
共线的单位向量是
)；
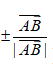4．相等向量：
长度相等且方向相同的两个向量叫相等向量，相等向量有传递性；
5．平行向量（也叫共线向量）：
方向相同或相反的非零向量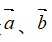
叫做平行向量，记作：
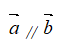，规定零向量和任何向量平行。
提醒：
①相等向量一定是共线向量，但共线向量不一定相等；
②两个向量平行与与两条直线平行是不同的两个概念：两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合；
③平行向量无传递性！（因为有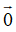
)；
④三点A、B、C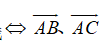共线
共线；
1.几何运算：
①向量加法：利用“平行四边形法则”进行，但“平行四边形法则”只适用于不共线的向量，如此之外，向量加法还可利用“三角形法则”：
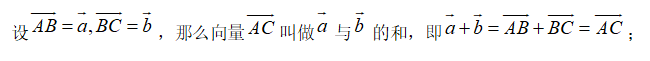
②向量的减法：用“三角形法则”：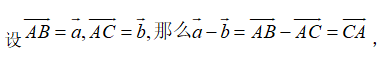
由减向量的终点指向被减向量的终点。注意：此处减向量与被减向量的起点相同。如：
（1）
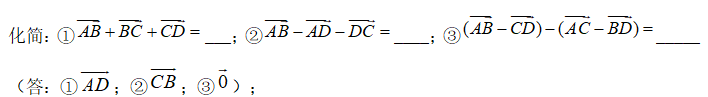
（2）
例题 ：
1.
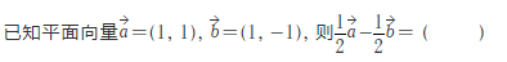
2.
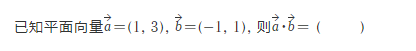
3.下面给出了关于复数的四种类比推理：
①若a,b∈R，则a-b＞0⇒a＞b”类比推出“若a,b∈C，则a-b＞0⇒a＞b”；
②复数的加减法运算可以类比多项式的加减法运算法则
③由实数a绝对值的性质|a|2=a2类比得到复数z的性质|z|2=z2；
④由向量加法的几何意义可以类比得到复数加法的几何意义．
其中类比得到的结论错误的是（ ）
A．①③ B．②④ C．②③ D．①④
4.下列是关于复数的类比推理：
①复数的加减法运算可以类比多项式的加减法运算法则；
②由实数绝对值的性质|x|²=x²类比得到复数z的性质|z|²=z²；
③已知a,b∈R，若a-b＞0，则a＞b.类比得已知z1，z2∈C，若z1-z2＞0，则z1＞z2；
④由向量加法的几何意义可以类比得到复数加法的几何意义．
其中推理结论正确的是①④．
解析：
1.
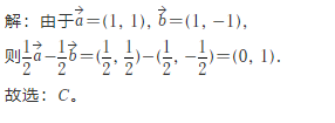
2.
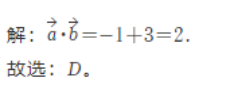
3.
解：①若a,b∈C，当a=1+i,b=i时，a-b=1＞0，但a,b 是两个虚数，不能比较大小．故错误；
②复数的加减法运算可以类比多项式的加减法运算法则，正确；
③由实数a绝对值的性质|a|2=a2类比得到复数z的性质|z|2=z2，不正确，比如z=i；
④由向量加法的几何意义可以类比得到复数加法的几何意义，正确．
故选：A．
4.
