考试内容 数列的概念、等差数列、等比数列 考试要求 (1)了解数列的概念。理解等差数列和等比数列的定义。 (2)理解等差中项公式、等差数列的通项公式与前 n 项和的公式。 (3)理解等比中项公式、等比数列的通项公式与前 n 项和的公式。 (4)会解简单的数列应用题。 一、数列 1.数列概念: 2.求数列的通向: 3.求数列的前n项和的基本方法: (1)公式法:利用等差数列或等比数列前n项和Sn公式; (2)分组求和:把一个数列分成几个可以直接求和的数列. (3)裂项(相消)法:有时把一个数列的通项公式分成两项差的形式,相加过程消去中间项,只剩有限项再求和. (4)错位相减:适用于一个等差数列和一个等比数列对应项相乘构成的数列求和. (5)倒序相加:例如,等差数列前n项和公式的推导. 二、等差数列 1.等差数列的概念: 如果一个数列从第二项起,每一项与前一项的差是同一个常数,那么这个数列久叫做等差数列,这个常数叫做等差数列的公差. 即 2.等差数列的通项公式: 3.等差中项: 4.等差数列的性质: 5. 6、等差数列前n和的性质: 7. 三、等比数列 1.等比数列的概念: 2.等比数列的通项公式: 3.等比中式: 4.等比数列的性质: 5.等比数列的前n项和: 6.等比数列的前n项和性质: 四、解数列应用题 1、零存整取模型: 银行有一种叫作零存整取的储蓄业务,即每月定时存入一笔相同数目的现金,这是零存;到约定日期,可以取出全部本利和,这是整取.规定每次存入的钱不计复利. 注:单利的计算是仅在原本金上计算利息,对本金所产生的利息不再计算利息.其公式为:利息=本金×利率×存期.以符号p代表本金,n代表存期,r代表利率,s代表本金和利息和(即本利和),则有s=p(1+nr). 零存整取是等差数列求和在经济方面的应用. 2、定期自动转存模型: 银行有一种储蓄业务为定期存款自动转存.例如,储户某日存入一笔1年期定期存款,1年后,如果储户不取出本利和.则银行自动办理转存业务,第2年的本金就是第1年的本利和. 注:复利是把上期末的本利和作为下一期的本金,在计算时每一期本金的数额是不同的.复利的计算公式是:s=p(1+r)n. 定期自动转存(复利)是等比数列求和在经济方面的应用. 3、分期付款模型: 分期付款要求每次付款金额相同外,各次付款的时间间隔也相同.分期付款总额要大于一次性付款总额,二者的差额与分多少次付款有关,且付款的次数越少,差额越大.分期付款是等比数列的模型. 采用分期付款的方法,购买售价为a元的商品(或贷款a元),,每期付款数相同,购买后1个月(或1年)付款一次,如此下去,到第n次付款后全部付清,如果月利率(或年利率)为b,按复利计算,那么每期付款x元满足下列关系: 例题 : 1.在1与25之间插入五个数,使其组成等差数列,则这五个数为( ) A.3,8,13,18,23 B.4,8,12,16,20 C.5,9,13,17,21 D.6,10,14,18,22 2.若a,b,c成等差数列,且公差不为0,则二次函数f(x)=ax²+2bx+c的图像与x轴交点的个数为( ) A.0 B.1 C.2 D.不确定 3. 4. 5. 6. 7. 8.甲、乙两人连续6年对某县农村养鸡业规模进行调查,提供两个不同的信息:①从第一年每个养鸡场现产1万只鸡上升到第6年平均每个鸡场生产2万只鸡,每一年生产鸡的只数成等差数列:②由第一年养鸡场数为30个减少到第六年的10个,每一年鸡场的个数也成等差递减数列。请根据以上提供的信息解答下列问题. (1)第二年养鸡场的个数及全县出产鸡的总数; (2)哪一年的养鸡规模最大(即只数最多)? 解析: 1. 2. 3. 4. 5. 6. 7. 8.

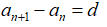 (常数),这也是证明或判断一个数列是否为等差数列的依据.
(常数),这也是证明或判断一个数列是否为等差数列的依据.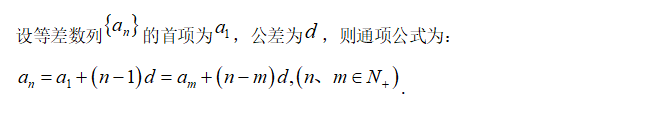


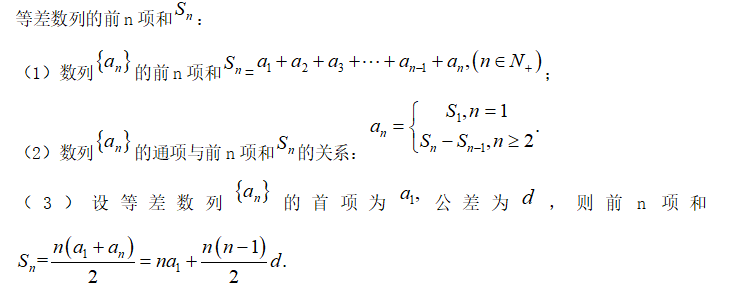



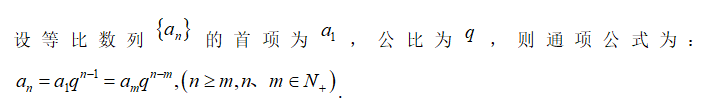
















2022年致尚职教高考共500名学子参加了3+证书高考,300分以上人数共计177人,300分优秀率达35.4%,2022年广东省3+证书高考人数12.3万人300分以上人数约11200人,优秀率仅9%,致尚职教高考优秀率是全省优秀率的3.93倍。
致尚升本www.zssbjy.com 聚焦于成人学历提升培训(高职高考、专插本、高考复读等),秉承“做好课程做好老师、做好服务”的价值主张,通过科学的管理、雄厚的师资力量、别具一格的教学特色,先后帮助了一批又一批学子圆梦大学。



