集合及其运算知识点
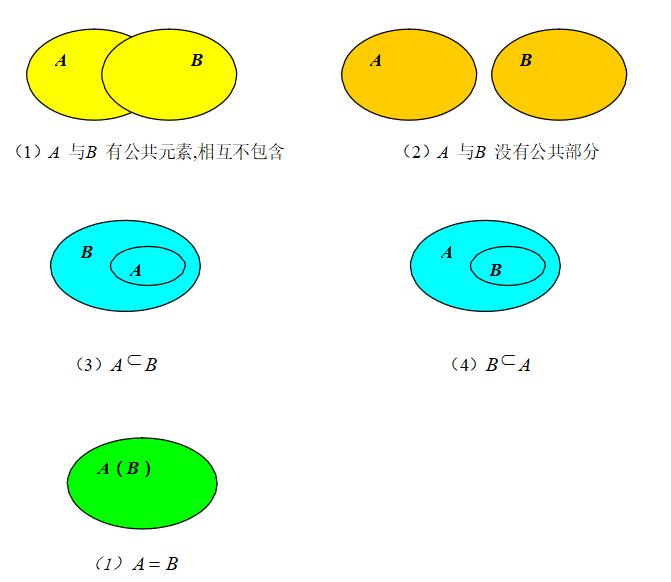
对并集的理解:
(1)求两个集合的并集是集合的一种运算,结果仍是一个集合,它是由属于集合 A或集合 B 的元素组成的.
(2)并集概念中的“ 或” 指的是只要满足其中一个条件即可, 符号语言“ x Î A, 或x Î B ”分为三种情况:
① x Î A ,但 x Ï B ; ② x Ï A ,但 x Î B ; ③ x Î A ,且 x Î B
(3)根据集合元素的互异性,在求两个集合的并集时,两个集合中的公共元素在并集中只能出现一次.
并集的性质:
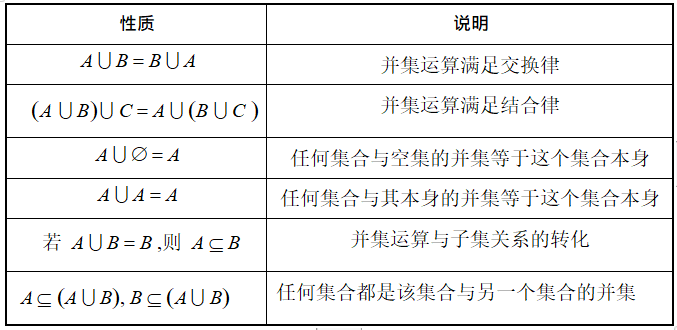
求并集的方法:
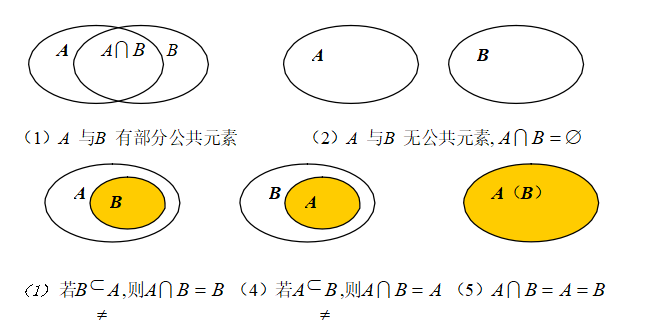
对交集的理解:
交集的性质:
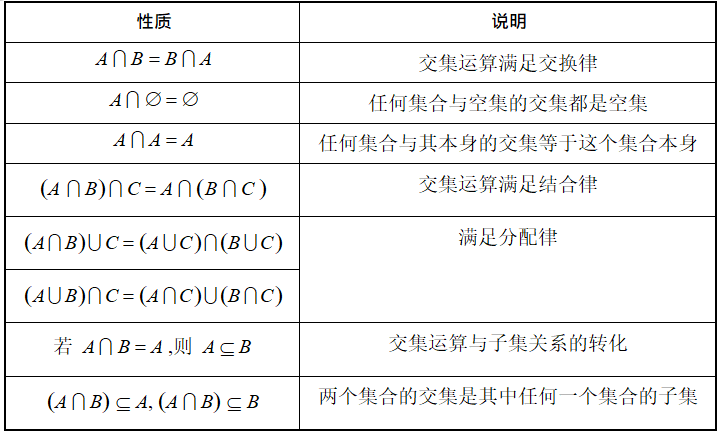
求交集的方法:
(1)求两个有限集的交集按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.
(2)求两个无限集的交集借助于数轴进行计算.两个集合的解集等于这两个集合在数轴上对应的图形所覆盖的公共范围.
相对于全集 U 的补集,简称集合 A 的补集,记作CU A,即:CU A = {x x ÎU , 且x Ï A}.
用 Venn 图表示为:
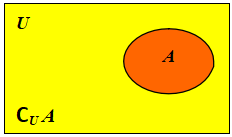
对补集的理解:
(1)补集是相对于全集而言的,求一个集合的补集,结果因全集的不同而不同.所以求补集前,要先明确全集.
(2)补集既是集合间的一种关系,同时也是集合之间的一种运算.
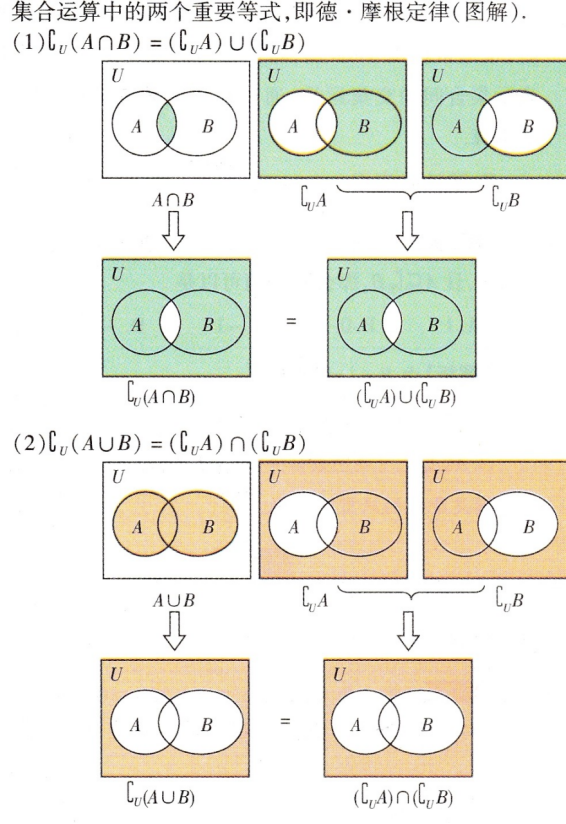
补集的性质:
如图所示,集合 A , B 将全集 U 分成了四部分,这四部分用集合表示如下:
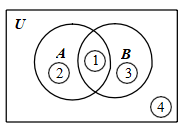

6.集合中元素的个数:
若集合 A 为有限集,则用 card(A)表示集合 A 中元素的个数.
如果集合 A 中含有m 个元素,那么有 card(A) = m .
(1)一般地,对于任意两个有限集合 A , B,有card (A U B) = card(A) + card(B)-card (A I B) .
(2)一般地,对于任意三个有限集合 A , B , C,有card (A U B U C ) = card(A) + card(B)-card (A I B) -card (A I C )-card (B I C )+card (A I B I C ) .
集合及其运算例题
例题:
1.已知集合A={-1,3,5},B={-2,3,5},则A∩B=( )
A.∅ B.{-1,-2} C.{-1,-2,3,5} D.{3,5}
2.已知集合A={x|-2<x≤1},B={-2,-1,0,1},则A∩B=( )
A.{-2,-1,0,1} B.{-1,0,1} C.{-1,0} D.{-2,-1,0}
解析:
1.解:∵集合A={-1,3,5},B={-2,3,5},
∴A∩B={3,5},
故选:D
2.解:∵集合A={x|-2<x≤1},B={-2,-1,0,1},
∴A∩B={-1,0,1}.
故选:B
每天学习一点点,每天进步一大点!
2022年致尚职教高考共500名学子参加了3+证书高考,300分以上人数共计177人,300分优秀率达35.4%,2022年广东省3+证书高考人数12.3万人300分以上人数约11200人,优秀率仅9%,致尚职教高考优秀率是全省优秀率的3.93倍。
致尚升本www.zssbjy.com 聚焦于成人学历提升培训(高职高考、专插本、高考复读等),秉承“做好课程做好老师、做好服务”的价值主张,通过科学的管理、雄厚的师资力量、别具一格的教学特色,先后帮助了一批又一批学子圆梦大学。



