考试内容
#01
平均值
平均值的概念很简单:所有数据之和除以数据点的个数,以此表示数据集的平均大小;其数学定义为:
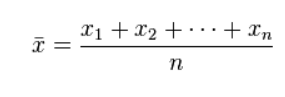
方差、标准差
方差这一概念的目的是为了表示数据集中数据点的离散程度;其数学定义为: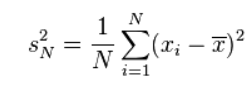
标准差与方差一样,表示的也是数据点的离散程度;其在数学上定义为方差的平方根: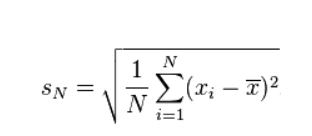
为什么使用标准差
与方差相比,使用标准差来表示数据点的离散程度有3个好处:1.表示离散程度的数字与样本数据点的数量级一致,更适合对数据样本形成感性认知。依然以上述10个点的CPU使用率数据为例,其方差约为41,而标准差则为;两者相比较,标准差更适合人理解。2.表示离散程度的数字单位与样本数据的单位一致,更方便做后续的分析运算。3.在样本数据大致符合正态分布的情况下,标准差具有方便估算的特性:%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内,而99%的数据点将会落在平均值前后3个标准差的范围内。【例题】
1.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )2.已知一组样本“x1,x2,…xn”的均值是3,标准差是3.5,则样本“4x1+2,4x2+2,…4xn+2”的均值为 标准差为 。
【解析】
1.解:A、总体均值为3,中位数为4时,不能限制某一天的病例超过7人,故A不符合该标志;B、总体均值为1,总体方差大于0时,不知道总体方差的具体数值,不能确定数据的波动大小,故B不符合该标志;C、中位数为2,众数为3时,也不能限制某一天的病例超过7人,故C不符合该标志;D、总体均值为2,总体方差为3时,若有一个数据超过7,则方差就接近3,故D符合该标志;
(来源:网络)
2022年致尚职教高考共500名学子参加了3+证书高考,300分以上人数共计177人,300分优秀率达35.4%,2022年广东省3+证书高考人数12.3万人300分以上人数约11200人,优秀率仅9%,致尚职教高考优秀率是全省优秀率的3.93倍。
致尚升本www.zssbjy.com 聚焦于成人学历提升培训(高职高考、专插本、高考复读等),秉承“做好课程做好老师、做好服务”的价值主张,通过科学的管理、雄厚的师资力量、别具一格的教学特色,先后帮助了一批又一批学子圆梦大学。
